试卷简介
本套试卷集合了考试编委会的理论成果。专家们为考生提供了题目的答案,并逐题进行了讲解和分析。每道题在给出答案的同时,也给出了详尽透彻的解析,帮助考生进行知识点的巩固和记忆,让考生知其然,也知其所以然,从而能够把知识灵活自如地运用到实际中去。
试卷预览
1.
要检验变量y和x之间的线性关系 是否显著,其中ɛ为随机误差,即考察由一组观测数据
是否显著,其中ɛ为随机误差,即考察由一组观测数据 ,得到的回归方程
,得到的回归方程 是否有实际意义,则需要检验假设 ()
是否有实际意义,则需要检验假设 ()
A、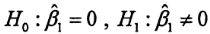
B、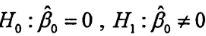
C、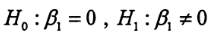
D、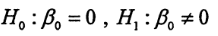
2.
设总体 为来自X的样本,为样本均值,s为样本标准差。则的无偏估计量为()
为来自X的样本,为样本均值,s为样本标准差。则的无偏估计量为()
A、s
B、s2
C、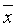
D、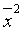
3.
设总体X~N(0,1),x1,x2,…,x5为来自X的样本,则 ( )
( )
A、N(0,5)
B、ᵡ2(5)
C、t(5)
D、F(1,5)
4.
设(X,Y)为二维随机变量,且D(X)>0,D(Y)>0, 为X与Y的相关系数,则Coy(X,Y)= ( )
为X与Y的相关系数,则Coy(X,Y)= ( )
A、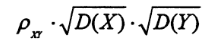
B、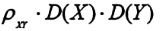
C、E(X)·E(Y)
D、D(X)·D(Y)
5.
设随机变量X服从二项分布B(10,0.6),Y服从均匀分布U(0,2),则E(X-2Y)=()
A、4
B、5
C、8
D、10

 最新推荐
最新推荐
 相关试卷
相关试卷

 原创试题专区
原创试题专区 开通学校服务
开通学校服务






